What is Six Sigma?

 

Six Sigma is a data-driven methodology that aims to reduce defects and improve process efficiency. 

Process improvement is the driving force behind organizational evolution, unlocking greater efficiency, quality, and innovation. It's the key to staying competitive, reducing waste, and ensuring progress toward excellence. Embracing process improvement isn't just a choice; it's imperative for businesses and institutions committed to continuous growth and success.

1. Understanding Six Sigma

What is Six Sigma?

Six Sigma is a quality management methodology that focuses on minimizing defects, reducing process variation, and improving efficiency. It follows a structured DMAIC approach and uses statistical tools to make data-driven decisions.

2. The DMAIC Methodology – The Core of Six Sigma Green Belt

The DMAIC process (Define, Measure, Analyze, Improve, Control) is the foundation of Six Sigma projects.

A. Define Phase (Problem Identification)

✔ Identify project goals and customer expectations (Voice of Customer – VoC)

✔ Develop a Project Charter (Problem Statement, Scope, Timeline)

✔ Use SIPOC (Suppliers, Inputs, Process, Outputs, Customers) to map the process

B. Measure Phase (Data Collection & Analysis)

✔ Identify Key Performance Indicators (KPIs)

✔ Create Flowcharts, Process Maps, and Value Stream Mapping (VSM)

✔ Collect data using Check Sheets, Pareto Charts

✔ Measure process performance using Process Capability (Cp, Cpk)

C. Analyze Phase (Root Cause Identification)

✔ Use Fishbone Diagram (Ishikawa) for root cause analysis

✔ Conduct Hypothesis Testing (T-tests, ANOVA, Chi-square)

✔ Perform Regression Analysis to identify relationships between variables

D. Improve Phase (Solution Development)

✔ Implement Design of Experiments (DOE) to test different solutions

✔ Use Kaizen (Continuous Improvement) and FMEA (Failure Mode Effects Analysis)

✔ Optimize processes using Lean Tools (5S, Kanban, JIT, Poka-Yoke)

E. Control Phase (Sustaining Improvements)

✔ Monitor process performance with Control Charts (SPC)

✔ Standardize the improved process with SOPs (Standard Operating Procedures)

✔ Train employees to sustain improvements

3. Statistical Tools for Six Sigma

 

1. Pareto Chart
When it is about the Six Sigma quality tools, the Pareto chart tops the list. This chart comes from the idea known as Pareto Principle. According to the Pareto Principle, nearly 80 percent of the outcome results from 20 percent of the cause. The Pareto chart is a special kind of bar chart that enable you to easily identify a few critical causes, thereby allowing you to focus on the vital issues.

2. Gage R&R
Gage R&R is one of the significant Sigma Six tools for process improvement. To solve a problem, accurate measurements are at the core. The Gage R&R allows you to determine whether the continuous measurements like pressure, weight, and diameter are reproducible and repeatable. It helps in checking the accuracy of the measurements

3.Histogram
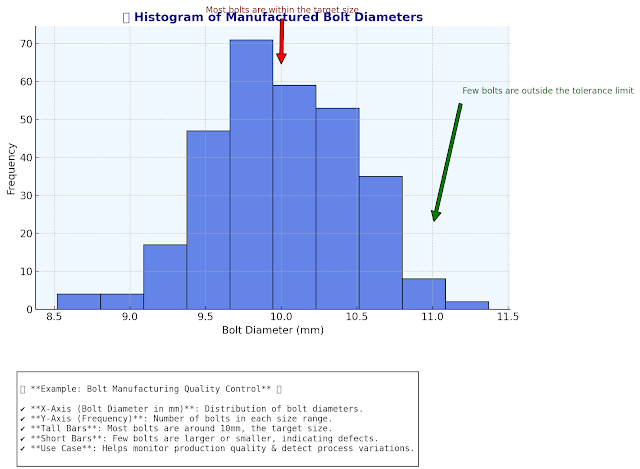
A histogram is one of the Six Sigma tools used for the process improvement of businesses. A histogram refers to a snapshot of continuous, numeric data. It allows you to identify the spread as well as the center of
data in much less time. It enables you to locate where maximum data fall and provide you with insights into the maximum and minimum value.

4. Process Capability
Every process has a specific upper and lower bound. The process capability analysis helps in quantifying how well a process can meet the set specifications. It can also provide you with an idea about the ways to improve the poor processes.

5. Attribute Agreement Analysis
Attribute agreement analysis is also one of the important Six Sigma analysis tools. It is an ideal tool for categorical assessments, like Fail or Pass. It allows you to determine whether the people rating the different categories agree with other appraisers, with themselves, as well as with known standards.

6. ANOVA
ANOVA is one of the popular Six Sigma tools that is widely used by organizations around the globe. It is a collection of statistical models that are used for the analysis of differences among mean. In simple words, this statistical tool enables you to compare two or more two means easily.

Example : Three types of fertilizers are used on three groups of plants for 5 weeks. We want to check if there is a difference in the mean growth of each group. Using the data given below apply a one way ANOVA test at 0.05 significant level.

Fertilizer 1	Fertilizer 2	Fertilizer 3
6	8	13
8	12	9
4	9	11
5	11	8
3	6	7
4	8	12

Solution:

$H_0$: ${\mu }_1$ = ${\mu }_2$ = ${\mu }_3$

$H_1$: The means are not equal

Fertilizer 1	Fertilizer 2	Fertilizer 3
6	8	13
8	12	9
4	9	11
5	11	8
3	6	7
4	8	12
${\overline{X}}_1$ = 5	${\overline{X}}_1$ = 9	${\overline{X}}_1$ = 10

Total mean, $\overline{X}$ = 8

$n_1$ = $n_2$ = $n_3$ = 6, k = 3

SSB = 6(5 - 8)² + 6(9 - 8)² + 6(10 - 8)²

= 84

df1 = k - 1 = 2

Fertilizer 1	(X - 5)2	Fertilizer 2	(X - 9)2	Fertilizer 3	(X - 10)2
6	1	8	1	13	9
8	9	12	9	9	1
4	1	9	0	11	1
5	0	11	4	8	4
3	4	6	9	7	9
4	1	8	1	12	4
${\overline{X}}_1$ = 5	Total = 16	${\overline{X}}_1$ = 9	Total = 24	${\overline{X}}_1$ = 10	Total = 28

SSE = 16 + 24 + 28 = 68

N = 18

df2 = N - k = 18 - 3 = 15

MSB = SSB / df1 = 84 / 2 = 42

MSE = SSE / df2 = 68 / 15 = 4.53

ANOVA test statistic, f = MSB / MSE = 42 / 4.53 = 9.33

Using the f table at $\alpha$ = 0.05 the critical value is given as F(0.05, 2, 15) = 3.68

As f > F, thus, the null hypothesis is rejected and it can be concluded that there is a difference in the mean growth of the plants.

Answer: Reject the null hypothesis

1

2

3

7. Regression
Regression is a Six Sigma statistical tool that is helpful in the determination of the existence of a relationship between one or more input variables and the output variable. For instance, using the tool, you can determine whether there is a relationship between the sales revenue and the marketing expenditure of a company. If there exists any relationship, you can make use of the regression equation for describing the relationship and predicting the values of future output for the provided input values.

     

 8. t-Tests

A t-test is another statistical tool that is used for comparing the average of one sample to the average of another sample. It can also be used for comparing the average of one sample to a given target.

9. Control Charts
The control chart is an important Six Sigma tool for risk analysis. To ensure the quality of services and products, it is vital to have a stable process. A control chart helps in distinguishing a special-cause variation from the natural and acceptable variation. It allows the identification of unusual variations, thereby allowing you to take the necessary actions.

Example Calculation (using an X-bar chart):

Data: Let's say we collect samples of 5 products each and measure their weight, resulting in the following data sets:

Sample 1: [10.2, 10.5, 10.1, 10.3, 10.4]

Sample 2: [10.0, 10.2, 10.1, 10.3, 10.4]

Sample 3: [9.8, 10.0, 10.2, 10.1, 10.3]

Calculate the average of each sample (X-bar):

Sample 1: (10.2 + 10.5 + 10.1 + 10.3 + 10.4) / 5 = 10.3

Sample 2: (10.0 + 10.2 + 10.1 + 10.3 + 10.4) / 5 = 10.2

Sample 3: (9.8 + 10.0 + 10.2 + 10.1 + 10.3) / 5 = 10.1

Calculate the overall average (Grand Mean):

(10.3 + 10.2 + 10.1) / 3 = 10.2

Calculate the range for each sample (difference between the highest and lowest value):

Sample 1: 10.5 - 10.1 = 0.4

Sample 2: 10.4 - 10.0 = 0.4

Sample 3: 10.3 - 9.8 = 0.5

Calculate the average range (R-bar):

(0.4 + 0.4 + 0.5) / 3 = 0.43

Determine the control limits using standard formulas (assuming a normal distribution):

Upper Control Limit (UCL) for X-bar: Grand Mean + (A2 * R-bar) = 10.2 + (0.577 * 0.43) = 10.4

Lower Control Limit (LCL) for X-bar: Grand Mean - (A2 * R-bar) = 10.2 - (0.577 * 0.43) = 10.0

UCL for R: D4 * R-bar = 2.282 * 0.43 = 0.98

LCL for R: D3 * R-bar = 0 * 0.43 = 0 (usually set to zero)

Interpreting the chart:

Plot the average of each sample (X-bar) on the X-bar control chart, and the range of each sample on the R chart.

If any points fall outside the calculated control limits, it may indicate a special cause of variation and further investigation is needed to identify the root cause. 

Key points about control charts:

Different types of control charts exist depending on the data being analyzed (e.g., X-bar and R chart, P chart for proportions, C chart for counts). 

Control charts are most effective when used with a consistent sampling plan and when the process is stable.

10. DOE

DOE, or Design of Experiments, is a branch of applied statistics that uses planning, conducting, analyzing, and interpreting controlled tests to explain the variation of information under conditions hypothesized to reflect the variation. It’s a powerful data collection and analysis tool that investigates how different factors or variables affect an outcome or response of interest.

Purpose of Experimentation

Designed experiments have many potential uses in improving processes and products, including:

• Comparing Alternatives. In the case of our cake-baking example, we might want to compare the results from two different types of flour. If it turned out that the flour from different vendors was not significant, we could select the lowest-cost vendor. If flour were significant, then we would select the best flour. The experiment(s) should allow us to make an informed decision that evaluates both quality and cost.
• Identifying the Significant Inputs (Factors) Affecting an Output (Response) - separating the vital few from the trivial many. We might ask a question: "What are the significant factors beyond flour, eggs, sugar and baking?"
• Achieving an Optimal Process Output (Response). "What are the necessary factors, and what are the levels of those factors, to achieve the exact taste and consistency of Mom's chocolate cake?
• Reducing Variability. "Can the recipe be changed so it is more likely to always come out the same?"
• Minimizing, Maximizing, or Targeting an Output (Response). "How can the cake be made as moist as possible without disintegrating?"
• Improving process or product "Robustness" - fitness for use under varying conditions. "Can the factors and their levels (recipe) be modified so the cake will come out nearly the same no matter what type of oven is used?"
• Balancing Tradeoffs when there are multiple Critical to Quality Characteristics (CTQC's) that require optimization. "How do you produce the best tasting cake with the simplest recipe (least number of ingredients) and shortest baking time?"

8 Wastes of Lean

4. Lean Principles in Six Sigma

Lean Six Sigma is a robust methodology that combines two distinct but complementary approaches: "Lean" and "Six Sigma." It's all about enhancing operational performance by reducing waste and improving quality.

Six Sigma Green Belt integrates Lean principles to eliminate waste. The 8 Wastes of Lean are:

1) Defects – Errors that require rework

2) Overproduction – Producing more than needed

3) Waiting Time – Delays in the process

4) Non-Utilized Talent – Employees not used effectively

5) Transportation – Unnecessary movement of materials

6) Inventory – Excess raw materials or finished goods

7) Motion – Unnecessary movement of workers

8) Extra Processing – Unneeded steps in production

Key Lean Six Sigma Tools

✔ 5S (Sort, Set, Shine, Standardize, Sustain) – Workplace organization

✔ Kanban & Just-In-Time (JIT) – Inventory management

✔ Poka-Yoke (Mistake Proofing) – Error prevention

5. Advanced Six Sigma Green Belt Concepts

A. Process Capability Analysis

Cp & Cpk – Measures how well a process meets specifications

Pp & Ppk – Evaluates long-term process performance

B. Design of Experiments (DOE)

Factorial Design – Testing multiple variables simultaneously

Taguchi Methods – Optimizing product and process design

C. Failure Mode & Effects Analysis (FMEA)

Identifies potential failures in a process

Assigns risk priority numbers (RPN)

The normal distribution, also known as the Gaussian distribution, is the most frequently used statistical distribution. 

The deviations of the (measured) values of many scientific, economic and engineering processes from the mean value can often be described in a good approximation by the normal distribution. Its probability density is a bell-shaped curve that runs symmetrically around the mean value (Gaussian bell curve). 

For some statistical analyses, the data must come from an approximately normally distributed population. The normal distribution is then used as a model for further data analyses.